Números y estadísticas no siempre representan la realidad

Menuda perla de titulo. Parece que avanzo concienzudamente en mi camino para convertirme en “maestro de lo obvio”, figura de la que da habida cuenta Scott Adams en su magnifico libro “El principio de Dilbert”.

Hace algunos días discutía con un compañero sobre las medias de desviación en horas de ciertos proyectos y, aunque parecían prometedoras, a mi no acababan de convencerme. Tras hacer un rato de espeleología algebraica, descubrimos que las medias eran completamente correctas… pero que inducían a engaño. A raíz de esta discusión se me ocurrió hablar sobre ello aquí y proponer una serie de reglas “mínimas” a aplicar cuando alguien ofrece un conjunto de datos, ya sea en porcentajes, gráficas u otro medio. Alegaré en mi defensa que no tengo conocimientos de estadística más allá de los normales, y que este planteamiento va orientado eminentemente a la práctica sencilla.

La realidad es que en nuestro día a día manejamos cada vez más datos agregados, calculados muchas veces utilizando fórmulas que no conocemos, y que son la base sobre la que debemos tomar decisiones de cierta importancia… Los datos en sí no son malos, ni aunque no sean completamente precisos. En mi opinión, es más importante que un dato sea significativo (representa lo mejor posible la realidad que pretende mostrar) que preciso (el dato mide la realidad sin ninguna desviación).

Una anécdota para ilustrarlo:

Yo soy aficionado a correr, y habitualmente utilizo un podómetro para estimar aproximadamente cuanta distancia he recorrido. Hace algún tiempo, un compañero de carrera me informó escandalizado que mi podómetro estaba desviado aproximadamente 60 metros por kilometro, y que por tanto no estaba entrenando apropiadamente. Le comenté que era algo que me preocupaba bastante poco, ya que lo que pretendía medir no era la distancia, sino como iba evolucionando día a día, es decir el delta… para lo cual, la desviación no es importante (si es siempre la misma, claro)

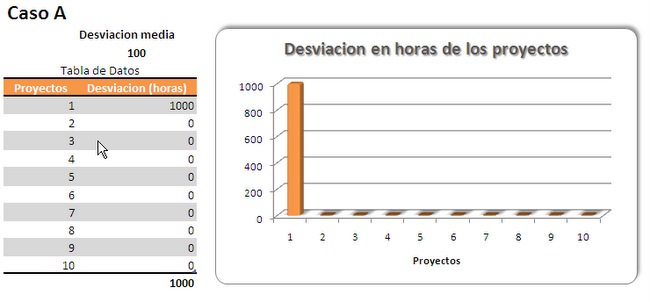
Para “abrir boca” y exponer el problema en toda su crudeza, he inventado una serie de datos ficticios sobre potenciales desviaciones en 3 escenarios con 10 proyectos, que curiosamente todos comparten una desviación media de 100 horas:

En el caso A, existe un sólo proyecto que acumula una desviación de 1.000 horas, y el resto se encuentran en estado nominal.

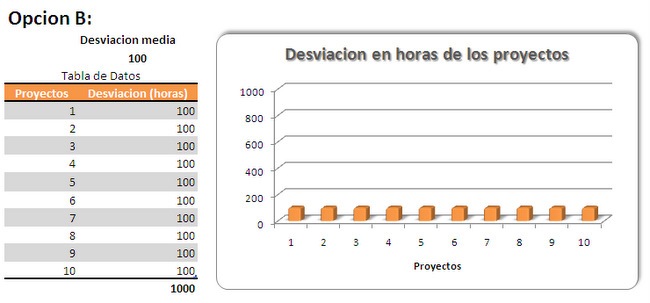
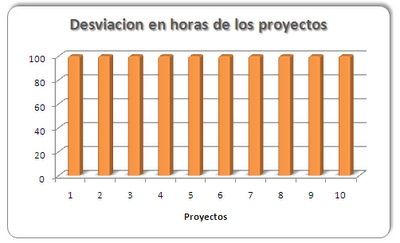
En el caso B, las desviaciones están homogéneamente distribuidas entre todos los proyectos con 100 horas.

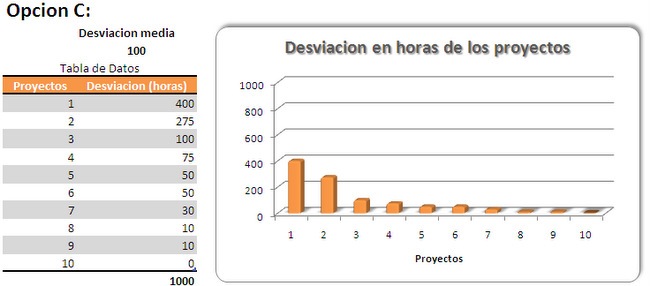
En el caso C sin embargo se da una distribución mas real, en la que existen 3 proyectos que acumulan el grueso de las desviaciones.

Como es fácil ver, ese dato (desviación media de proyectos = 100 horas) podría representar infinitas realidades… lo que haría que tomar una decisión en base sólo a ello sería desastroso. En consecuencia, podemos empezar ya a plantear algunas reglas mínimas:

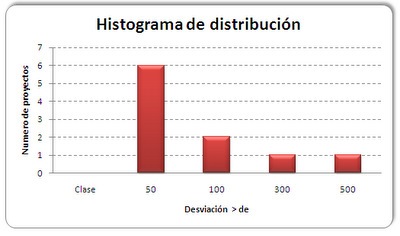
• Jamás debemos aceptar un dato de media a secas, sino que deberemos pedir la distribución de los datos que dan origen a esa media, o incluso mejor, un histograma ponderado con la distribución. Por ejemplo, para el caso C sería:

Algunas otras reglas importantes:

• Cuando intentemos averiguar la media “normal” de un valor, por ejemplo cual]}**es son nuestros ingresos mensuales (si estos son muy variables, como sucede en el caso de determinados autónomos) se deben quitar los 3 valores más altos y los 3 mas bajos, y sacar la media con estos datos. El objetivo es que el “ruido” estadístico provocado por su presencia no afecte al resultado final.

• En el caso de una conclusión sacada de una estadística, es extremadamente importante que identifiquemos el tamaño y la muestra de la población sobre la que se ha hecho la estadística. Un ejemplo: Mi suegra dice que todos los gallegos son altos, rubios y de ojos claros porque bastantes familiares suyos de allí tienen esas características… ¿pero es suficiente la población estudiada para tomar esa determinación?. En general ante cualquier estadística debemos pedir tamaño y características de la población y su comparación con el total de la población existente.

• Cuando se esté analizando una gráfica, es muy importante fijarse en las magnitudes de los ejes. Por ejemplo, la herramienta Excel tiende a modificar automáticamente los ejes para que representen el valor máximo de la serie, lo que puede llevar a tomar conclusiones equivocadas comparando gráficos. Un ejemplo: En el Caso B, Excel ofrece el siguiente formato de gráfico por defecto, en lugar del que he puesto anteriormente, que si comparásemos con el del Caso A, podríamos considerar que el Caso B es mucho peor… En general, si es un gráfico que se va a comparar es recomendable que los máximos y mínimos de los ejes sean fijos.

• Por coherencia, en los gráficos que aparezca la evolución de un elemento en el tiempo, deberíamos representar siempre en el eje X el tiempo, que transcurre de izquierda a derecha, y en el eje Y el valor que evoluciona. Aunque parezca de perogrullo, me he encontrado varios gráficos que no están creados así

• Cuando se comparen datos en una gráfica, hay que fijarse en sobre que valores se compara: No es lo mismo comparar con el valor del mes anterior (posiblemente más relacionado con el valor del mes actual) que con el mejor o peor valor de toda la historia. El aspecto e interpretación por defecto del gráfico cambia de forma completa.

Os recomiendo para complementar esta lectura el post “Verdades y mentiras de las estadísticas”, del interesante blog “Estrategia Digital”, en el que se hace hincapié en que lo importante es ser crítico respecto a la información mostrada y, por tanto, en la percepción que se produce de la misma.

Como decía Groucho Marx con tono ofendido:

A quien piensa creer usted…¿a mi o a sus propios ojos?

ACTUALIZACION (17/11/09): He encontrado éste estupendo esquema sobre qué gráfico utilizar en función de la información que queramos mostrar (composición de la muestra, comparaciones, relaciones…etc). En Juice Analytics disponen de un asistente básico, pero que permite exportar los diversos tipos de gráfico a Excel para tener un punto de partida de calidad.